4730. Фибоначчи
Числа Фибоначчи –
это последовательность
чисел f(n), которая задаётся формулой:
·
f(0) = 1,
·
f(1) = 1,
·
f(n) = f(n – 1) + f(n – 2)
По заданному
числу n выведите n-ое число Фибоначчи.
Вход. Неотрицательное число n (n ≤ 45) – номер
числа Фибоначчи, которое следует вывести.
Выход. Выведите n-ое
число Фибоначчи.
|
Пример
входа |
Пример
выхода |
|
4 |
5 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
Вычислим все
числа Фибоначчи и поместим их в массив fib, установив fib[i] = f(i). Затем выведем требуемое число
Фибоначчи.
Пример
Массив fib будет
заполнен следующим образом:

Реализация алгоритма
Будем вычислять
числа Фибоначчи и сохранять их в массиве fib: fib[i] = f(i).
#define MAX 46
int fib[MAX];
Заполняем массив fib в соответствии с рекуррентной формулой.
fib[0] = 1;
fib[1] = 1;
for (int i = 2; i < MAX; i++)
fib[i] = fib[i-1] + fib[i-2];
Читаем входное значение n. Выводим ответ.
scanf("%d",&n);
printf("%d\n",fib[n]);
Реализация алгоритма –
рекурсия
Для хранения чисел Фибоначчи объявим массив fib: fib[i]
= f(i).
#define MAX 46
int fib[MAX];
Рекурсивная функция f вычисляет n-ое число Фибоначчи. Используем технику мемоизации.
int f(int
n)
{
if (n <=
1) return 1;
if (fib[n] !=
-1) return fib[n];
return fib[n]
= f(n-1) + f(n - 2);
}
Основная часть программы. Читаем число n.
scanf("%d",&n);
Присвоим всем элементам массива fib значение -1.
memset(fib,-1,sizeof(fib));
Вычисляем и выводим значение f(n).
printf("%d\n",f(n));
Реализация алгоритма –
итерация
Читаем входное число n.
scanf("%d", &n);
Обрабатываем базовый случай.
if (n == 0 || n == 1)
{
printf("1\n");
return 0;
}
Занесем:
·
В переменную a нулевое число Фибоначчи;
·
В переменную b первое число Фибоначчи;
Изначально переменные a и b содержат два последовательных числа Фибоначчи.
a = b = 1;
for (i = 2; i <= n; i++)
{
Переменные a и b содержат два последовательных числа Фибоначчи:
a = f(i
– 2),
b = f(i
– 1)
Вычисляем следующее число Фибоначчи:
c = a
+ b = f(i – 2) + f(i
– 1) = f(i)
c = a + b;
Совершаем сдвиг, в результате которого a = f(i – 1) и b = f(i).
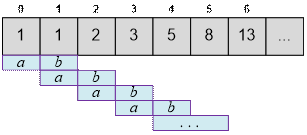
a = b;
b = c;
}
Выводим ответ. Переменная
b содержит значение f(n).
printf("%lld\n", b);
Java реализация
import java.util.*;
public class Main
{
public static int MAX =
46;
static int fib[] = new int[MAX];
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
fib[0] =
1; fib[1] = 1;
for(int i = 2;
i < MAX; i++)
fib[i] = fib[i-1] +
fib[i-2];
System.out.println(fib[n]);
con.close();
}
}
Java реализация – константная
память
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int a = 1,
b = 1, temp;
for(int i = 0;
i < n; i++)
{
temp = a;
a = b;
b = temp + b;
}
System.out.println(a);
con.close();
}
}
Java реализация – рекурсия, TLE
import java.util.*;
public class Main
{
static int f(int n)
{
if (n <= 1) return 1;
return f(n-1) + f(n - 2);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
System.out.println(f(n));
con.close();
}
}
Java реализация – рекурсия с
запоминанием
import java.util.*;
public class Main
{
static int fib[] = new int[46];
static int f(int n)
{
if (n <= 1) return 1;
if (fib[n] != -1) return fib[n];
return fib[n] = f(n-1) + f(n - 2);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
Arrays.fill(fib, -1);
System.out.println(f(n));
con.close();
}
}
Python реализация – список
Для хранения чисел Фибоначчи объявим список fib: fib[i] = f(i).
fib = [1,1]
Заполняем список fib в соответствии с рекуррентной
формулой.
for i in
range(2,46):
fib.append(fib[i-1] + fib[i-2])
Основная часть программы. Читаем число n.
n = int(input())
Вычисляем и выводим значение f(n).
print(fib[n])
Python реализация – константная память
n = int(input())
a, b = 1, 1
for i in
range(n):
a, b = b, a + b
print(a)
Python реализация – запоминание
Для хранения чисел Фибоначчи объявим список fib: fib[i] = f(i).
fib = [-1] * 46
Рекурсивная функция f вычисляет n-ое число Фибоначчи. Используем технику мемоизации.
def f(n):
if n <= 1: return 1
if fib[n] != -1: return fib[n]
fib[n] = f(n - 1) + f(n
- 2)
return fib[n]
Основная часть программы. Читаем число n.
n = int(input())
Вычисляем и выводим значение f(n).
print(f(n))